Liftoff and the Natural Rate of Interest
Markets have become focused on if and when the Federal Reserve should "liftoff"—that is, depart from its zero interest rate policy. This essay examines the issue by drawing on two concepts from a central banker's toolkit: the natural rate of interest and monetary policy rules.
Simply put, an interest rate is a price at which borrowers and lenders exchange dollars today for dollars at some point in the future. These trades occur in terms of dollars, so economists refer to this as a nominal interest rate to distinguish it from a real interest rate, which is the price at which goods today can be exchanged for equivalent goods at some point in future.1 The difference between a nominal interest rate and a real interest rate is the increase in the dollar price of goods (as well as services)—that is, the inflation rate. Hence, if goods become more expensive between the time someone lends money and is repaid, then the real rate of return earned on the loan is diminished.2
When assessing monetary policy, central bankers often consider the natural real interest rate (or natural rate). This natural rate has been described in technical terms as "the real interest rate consistent with output equaling the natural rate of output and stable inflation."3 The natural rate, sometimes also referred to as the equilibrium real interest rate, is a conceptual construct and cannot be directly measured the way nominal interest rates and stock prices can be.
Despite this measurement problem, the natural rate is viewed in some circles as a useful concept for the FOMC in setting the federal funds rate. The Federal Reserve can achieve its dual mandate if, tautologically according to the above definition, it can get the actual real interest rate to equal the natural rate. Because there are costs associated with rapid interest rate changes, a central bank may prefer to move the actual rate toward the natural rate gradually.

So the $64,000 question is, What is the value of the natural rate today? Opinions differ. I'll discuss a few possible ways to calculate the natural rate and draw out some implications for monetary policy.
John Taylor of Stanford University, the economist who first applied the natural rate to a specific, practical monetary policy rule, sets its value at 2 percent.4 His formula is known as the Taylor rule, which he argues the Fed should use for setting the federal funds rate. The natural rate, often represented as r*, is one component of that formula.5
Taylor also makes the case that, in periods of successful monetary policy, the federal funds rate has closely tracked the rate implied by the Taylor rule. In his view, the Taylor rule is both descriptive of these successful episodes (from a macroeconomic perspective) in the past and also prescriptive for the future.
The green line in the figure plots the real interest rate implied by Taylor's rule for 1995-2014, where r* equals 2 percent. The dark blue line plots the historical federal funds rate (in real terms). The real federal funds rate is constructed as the federal funds rate (i.e., a nominal interest rate) minus the inflation rate.6
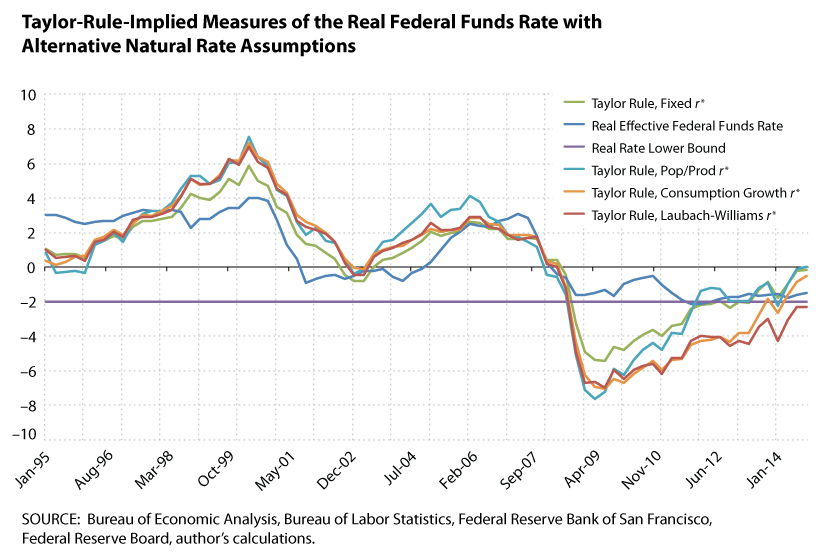
The nominal federal funds rate is bounded below by zero, but this zero bound doesn't imply a lower bound on the (expected) real interest rate. However, if inflation expectations are well-anchored at least in the short run, then the short-term real rate could be considered to also have a lower bound.7
I plot a "real rate lower bound" as the purple horizontal line at –2 percent: Since I plotted the Taylor-rule-implied rate and historical federal funds rate in real terms, I plot the lower bound on the interest rate in real terms as well. I choose –2 percent because the real rate is the nominal rate minus inflation. Furthermore, the nominal rate is zero at its lower bound and the FOMC's stated inflation target is 2 percent.
Three things jump out when examining the post-2007 side of the figure. First, the Taylor rule rate falls dramatically below the lower bound during the financial crisis. This occurs primarily because one ingredient in the Taylor rule, besides r*, is the deviation of output from its potential. When output declined during the recession and stayed below its long-run historical trend, the Taylor rule implied that the real rate should fall substantially below zero.
Second, the actual federal funds rate does not track the Taylor rule rate at this time because of the lower bound on interest rates. While the Taylor rule called for dramatic policy accommodation, this eventually became infeasible because of the lower bound.
Third, over the past year or so, the Taylor rule rate has been above the lower bound, since the gap between actual and potential output closed as the economy recovered. Essentially, this means that if one were to use the Taylor rule to conduct monetary policy, then the lower bound on interest rates no longer binds and, thus, the time has come for the Fed to begin to lessen its accommodative stance by raising the federal funds rate.
Another view is that the natural rate changes, possibly dramatically, over time in response to fundamentals. Based on the theory of economic growth, the real interest rate increases as the growth rates of productivity and the population increase.8,9 One simple approach to estimating the natural rate is to use these productivity and population measures of the real interest rate. In contrast to Taylor's formulation, this approach implies one should treat r* as time-varying in the Taylor rule because productivity and population growth change over time. Moreover, it is relatively straightforward to calculate r*, under the above assumptions, since its two components are observable.10
With an estimate of the population-productivity-based r* in hand, one can apply the Taylor rule with only one difference: Taylor's constant r* is replaced by a time-varying r*. The blue line in the figure plots the interest rate implied by a Taylor rule that uses the population-productivity-based r*. Over the past 10 years (with the exception of one year beginning in mid-2009), Taylor rules based on the constant r* and population-productivity-based r* have tracked each other very closely. The main implication here is that the policy rate implied by this Taylor rule is above the lower bound—and also above the current real effective federal funds rate over the past year. Thus, the population-productivity-based r* rule also prescribes that the FOMC should begin to raise the federal funds rate.
But there's more than one way (or even two ways) to skin a cat. Another calculation of the natural rate that also has theoretical underpinnings emerges from the observation that the real interest rate equals the growth rate of per capita consumption, as described in many economic models.11 The natural rate and the actual real interest rate can differ, however, because of frictions such as nominal price rigidities. One way to control for these frictions is to use a smoothed series for consumption growth rather than actual consumption growth in calculating the natural rate. So the consumption-growth-based r* here is estimated as the annualized consumption growth rate over the preceding 5 years.
We can also apply the Taylor rule using the consumption-growth-based r*. The orange line in the figure is the federal funds rate derived from this version of the Taylor rule, which puts the policy rate well above the current real effective funds rate and the real rate lower bound. Thus, the rule based on the consumption-growth r* also prescribes that the FOMC should begin to raise the federal funds rate.
In our final measure of the natural rate, we look to John Williams, president of the Federal Reserve Bank of San Francisco, and Thomas Laubach, Director of Monetary Affairs of the Board of Governors: Their alternative method for estimating a time-varying r*12 is constructed, in part, with a statistical technique known as Kalman filtering. I plot the federal funds target rate implied by the Taylor rule using the Laubach-Williams r*: the red line in the figure. For most of the sample, the Laubach-Williams-implied interest rate tracks the other Taylor rule policies very closely. The most significant departure occurs in the past two years.
The interest rate implied by the Taylor rule using this final natural rate measure shows a much smaller increase coming out of the most recent economic downturn than the other three rules show. Moreover, that rate currently remains below the lower bound (purple line), which suggests that this formulation of the Taylor rule implies the time has not yet come for the Fed to begin raising the interest rate.
The above exposition on liftoff and the natural rate isn't purely academic. Board of Governors Chair Janet Yellen in recent public communications has discussed the Taylor rule in the context of time-varying natural rate models.13 The natural rate model that gets the most discussion in her piece is that of Laubach and Williams.
Taylor's rule now calls for the federal funds rate to be well above zero if the unemployment rate is currently judged to be close to its normal longer-run level and the "normal" level of the real federal funds rate is currently close to its historical average. But the prescription offered by the Taylor rule changes significantly if one instead assumes, as I do, that appreciable slack still remains in the labor market, and that the economy's equilibrium real federal funds rate—that is, the real rate consistent with the economy achieving maximum employment and price stability over the medium term—is currently quite low by historical standards.
John Taylor has also recently weighed in:
So the main argument is that if one replaces the equilibrium federal funds rate of 2% in the Taylor rule with 0%, then the recommended setting for the funds rate declines by two percentage points […] In my view, there is little evidence supporting it, but this is a huge controversial issue, deserving a lot of explanation and research which I hope the Fed is doing or planning to do.14
Monetary policy rules provide useful yardsticks against which to compare actual FOMC policy actions. This is especially true of the Taylor rule, an essential component of which is the natural rate. I have examined four Taylor rules, which each use a distinct measure of the natural rate. Several of the measures have clear theoretical underpinnings that, at the same time, involve relatively straightforward calculations. All except one of the four place their corresponding Taylor-rule-prescribed target rates above the current federal funds rate as well as the lower bound. Therefore, all but one suggest that the time for liftoff has come.
Notes
1 Wages and gross domestic product are two other economic variables for which there is a nominal/real distinction.
2 In reality, the price of goods in the future and therefore the inflation rate between today and the future are not known with certainty; therefore, economists often refer to the expected real interest rate, which is the nominal interest rate minus the expected inflation rate.
3 Laubach and Williams (2003). The concept of the natural rate of interest is normally associated with Swedish economist Johan Gustaf Knut Wicksell (1851-1926).
4 In his work, Taylor refers to it with a different name: the equilibrium federal funds rate. See Taylor (1999).
5 A common version of the Taylor rule is
Rt = r*+ π* + 1.5 × (πt – 2) + (yt – yt)/yt
where Rt is the nominal interest rate, πt is inflation, π* is the target inflation rate, yt is real gross domestic product (GDP), and yt is potential real GDP. The rule is described in John Taylor (1999).
6 I measure inflation using the year-over-year change in the CPI (less food and energy).
7 The concept of a real rate lower bound is a loose one since this lower bound can be breached. In an environment with stable inflation and expected inflation, however, one shouldn't see prolonged periods of a real rate being below the real lower bound.
8 For a detailed discussion, see Poole's 2003 speech "Economic Growth and the Real Interest Rate" at https://fraser.stlouisfed.org/scribd/?item_id=1889....
9 Formally, this real interest rate relationship applies in the steady state of a Solow growth model where consumption per capita is set according to the so-called golden rule.
10 The population is measured as the civilian noninstitutional population over 16 years of age. Productivity is measured as business sector total factor productivity. Both growth rates are calculated as the 12-quarter average of annualized rates of growth for each quarter. I thank Kevin Kliesen for providing the population-productivity-based r* measures and underlying data.
11 Formally, this real interest rate relationship applies in a representative agent growth model when preferences over per capita consumption are time separable and the intertemporal elasticity of substitution equals one. With this approach, the natural rate also depends on households' "rate of time preference," which in most economic models is time invariant. I assume this term equals zero in these calculations. Adding a constant rate of time preference simply shifts up natural rate values, making it less likely that the natural rate lies below the lower bound.
12 See Laubach and Williams (2003). Their baseline estimates, updated through the end of 2014, are available at http://www.frbsf.org/economic-research/economists/.... See also Williams (2015).
13 See Yellen's (2015) speech "Normalizing Monetary Policy: Prospects and Perspectives."
14 http://economicsone.com/2015/03/29/was-janet-yelle...
References
Laubach, Thomas and Williams, John C. "Measuring the Natural Rate of Interest." Review of Economics and Statistics, February 2003, 85(4), pp. 1063-70.
Poole, William. "Economic Growth and the Real Rate of Interest." Bryant College, Providence, RI, October 14, 2003.
Taylor, John B. "A Historical Analysis of Monetary Policy Rules," in Monetary Policy Rules, University of Chicago Press, 1999, pp. 319-48.
Williams, John C. "The Decline in the Natural Rate of Interest." March 2015, Federal Reserve Bank of San Francisco; http://www.frbsf.org/economic-research/economists/....
Yellen, Janet. "Normalizing Monetary Policy: Prospects and Perspectives." March 17, 2015; http://www.federalreserve.gov/newsevents/speech/ye....
© 2015, Federal Reserve Bank of St. Louis. The views expressed are those of the author(s) and do not necessarily reflect official positions of the Federal Reserve Bank of St. Louis or the Federal Reserve System.


 follow @stlouisfed
follow @stlouisfed