Abstract

With a zero-knowledge proof (ZKP), a party can prove that a statement is true without revealing any information except for whether it is indeed true or not. The obvious benefit is privacy since the prover does not need to reveal any additional information, and the second benefit is that it can significantly reduce the cost of verifying the correctness of a statement. ZKPs are increasingly adopted in blockchain applications, where privacy and efficiency still have a lot of room for improvement. While it is expected that ZKP technology will also become ubiquitous in many other areas, the term remains cryptic to many people without a computer science background. In this review article, we shed light on what ZKPs are and how they improve privacy and efficiency and describe applications for blockchains and other use cases.

Aleksander Berentsen is a professor of economic theory at the University of Basel and a research fellow at the Federal Reserve Bank of St. Louis. Jeremias Lenzi is a PhD student at the University of Basel. Remo Nyffenegger is a PhD student and research assistant at the Center for Innovative Finance at the University of Basel. 

INTRODUCTION

Efficiency in economics means that scarce resources should not be wasted. This statement is true for manufacturing as well as for computations since they use real resources such as hardware, electricity, or human capital. There are various applications in which a computation's correctness must be verified by many other parties. For example, in blockchains, decentralization requires that many network participants recompute the correctness of each block that is appended to the chain. Obviously, reexecuting the same computations is inefficient because it involves using computational resources repeatedly.

By using a zero-knowledge proof (ZKP), a party can prove to other parties that a computation was executed correctly. There is no need to replicate the computation—only the proof needs to be verified. Ideally, verifying a ZKP  needs significantly less resources than reexecuting the computation. This benefit is illustrated in Figure 1; note that the efficiency gains of ZKPs increase linearly in the number of validators. 

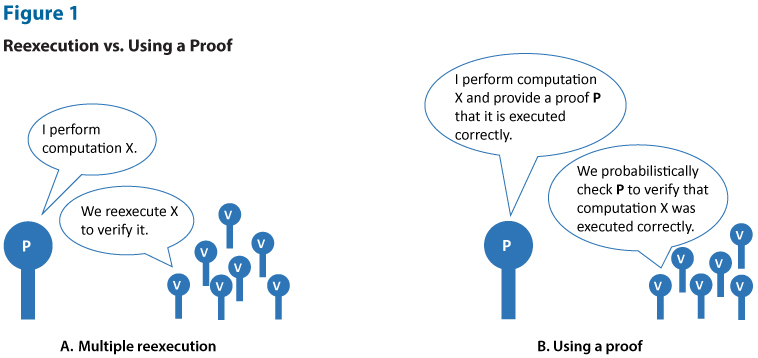
The second and more obvious benefit of ZKP technology is privacy. By using a ZKP, one can prove the correctness of a computation without revealing any additional information except for whether it is indeed correct or not. For example, a blockchain user can prove that he is indeed allowed to make a payment without revealing his identity to the network. Existing applications are the privacy-protecting cryptocurrency Zcash and the Tornado cash protocol on Ethereum (see Nadler and Schaer, 2023). The privacy and confidentiality of data is also important outside of blockchains. Two examples are a person who wants to prove that she voted without revealing her vote, or a company that wants to prove its solvency without revealing its balance sheet.

The theoretical concept of ZKPs was introduced in the late 80s by Goldwasser, Micali, and Rackoff, 1989. Conceptually, there are many different use cases, but none of them have become economically important. This has changed with the advent of blockchain technology, where ZKP technology has been integrated in some applications. ZKP research is rapidly expanding as demonstrated by the increasing number of articles about the technology (see Burger et al., 2022 for an overview). 

Most research on ZKPs targets an audience with a computer science or mathematics background, and there is a lack of a comprehensive but intuitive introduction into the topic. This review article fills this gap by providing an accessible but extensive introduction into zero knowledge proofs and their applications. Furthermore, in Berentsen, Lenzi, and Nyffenegger, 2022 we provide a comprehensive example of a ZKP that includes more advanced math and comes with an accompanying Python script.

Read the full article.